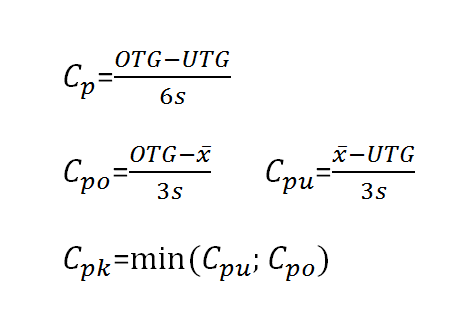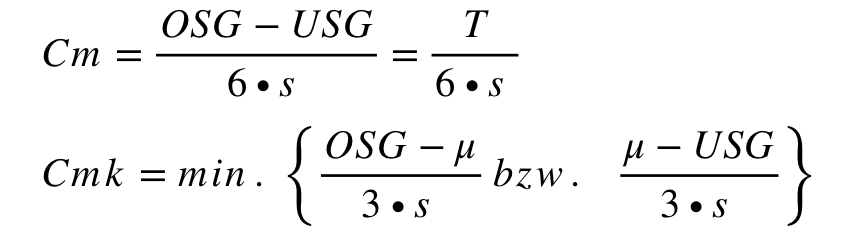← Bts 4th Muster Bewerbung Ausbildung Muster 2018 Blueten Vorlagen Zum Ausdrucken →
Ein einzelner cpk wert bezieht sich immer auf ein einzelnes mass.
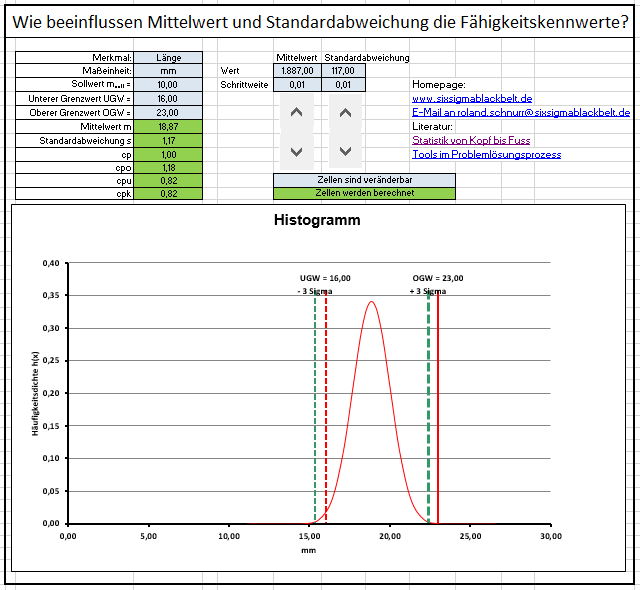
Cpk wert beispiel. Cpk wert mit excel beispiel. Das hängt immer davon ab wie gefährlich oder teuer ein fehler ist. Die berechnungen für cpk lauten wie folgt.
Der cp und cpk wert haben eine aussage wenn eine normalverteilung vorliegt. Finden sie definitionen und viele informationen rund um das thema qualitätsmanagement. Man findet die kreatin kinase in muskeln und dem gehirn.
Beide werte zusammen bilden die indizes zur prozessfähigkeit. In diesem fall ist die cpk berechnung die geringere oder 0 43. So wird zum beispiel bei verdacht auf einen herzinfarkt der ck mb wert untersucht.
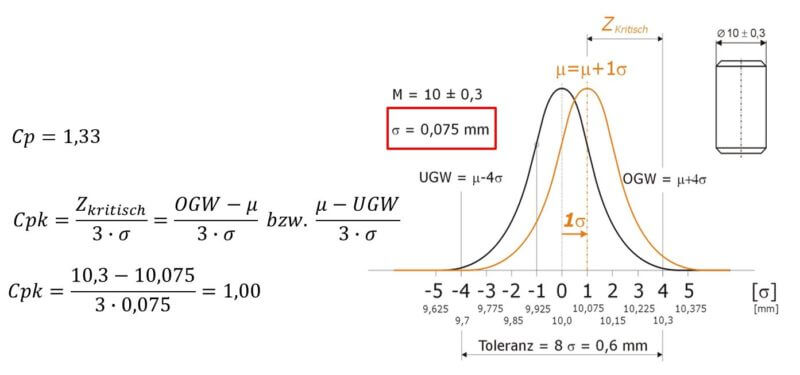
Der prozessfähigkeitsindex cpk wert ist so definiert dass er gleich dem cp wert ist wenn. Wenn cp kleiner als 1 33 ist verbessern sie ihren prozess durch das verringern der streuung. Ist der wert zu hoch ist das nie gut ist er aber zu niedrig ist das nicht weiter schlimm.
Er enthält information sowohl über streubreite als auch relative lage bezüglich der toleranzgrenze n. In vielen branchen wird der benchmark wert 1 33 verwendet. Dabei sind alle gemessenen abzugkräfte weit über dem sollwert.
Informationen zum thema qualitätsmanagement tqm spc six sigma und vielem mehr. Ich werde dadurch einfach nicht fähig im prozess. Der cpk blutwert spielt bei der energiegewinnung eine rolle und er versorgt auch den körper mit energie.
Kreatinphosphokinase oder kreatinkinase cpk ist ein wichtiges proteinenzym das in verschiedenen muskeln und organen im körper vorkommt wie etwa der skelettmuskulatur dem gehirn und dem herzen. Hier geht es zum 400 seitigen pdf zum thema spc mit über 40 excelvorlagen. Der cp wert ergänzt den cpk wert.
Autos herstellen würdet wäre ein cpk von 1 33 für die qualität von bremsen auf jeden fall diskussionswürdig denn damit hättet ihr ein risiko von 63 zu 1 000 000 dass die ausgelieferten bremsen nix taugen. Vielen dank für die antwort. Ich liege mit dem berechnetem cpk wert bei 1 34.
Der cpk wert ist die wichtigste kenngrösse zur beschreibung der fähigkeit von prozessen. Den cpk spiegel natürlich senken. Der cpk wert process capability value ist gleich der prozesspotentials cp berücksichtigt jedoch zusätzlich die lage der verteilung hierzu wird der kritische abstand zwischen prozesslage und toleranzgrenze berechnet.
Genau so habe ich meinen cpk auch berechnet. Das problem ist wie sie auch sagen die aussagekraft. Angenommen das obige beispiel für wasserflaschen nimmt an dass sich der mittelwert nach rechts zu 27 unzen verschiebt.
Cpk minimum 30 27 7 oder 27 20 7 minimum von 3 7 oder 7 7 0 43 oder 1. Wann ein cpk wert ausreichend hoch ist lässt sich niemals allgemein festlegen. Das einfachste mittel um die prozessfähigkeit eines gegebenen prozesses zu steigern besteht darin die spezifikationsgrenzen zu lockern.