← Artikel 13 Dsgvo Muster Beitrittserklärung Verein Muster Auflösungsbeschluss Gmbh Muster →
6 n3 6n2 14n ist durch 3 teilbar.
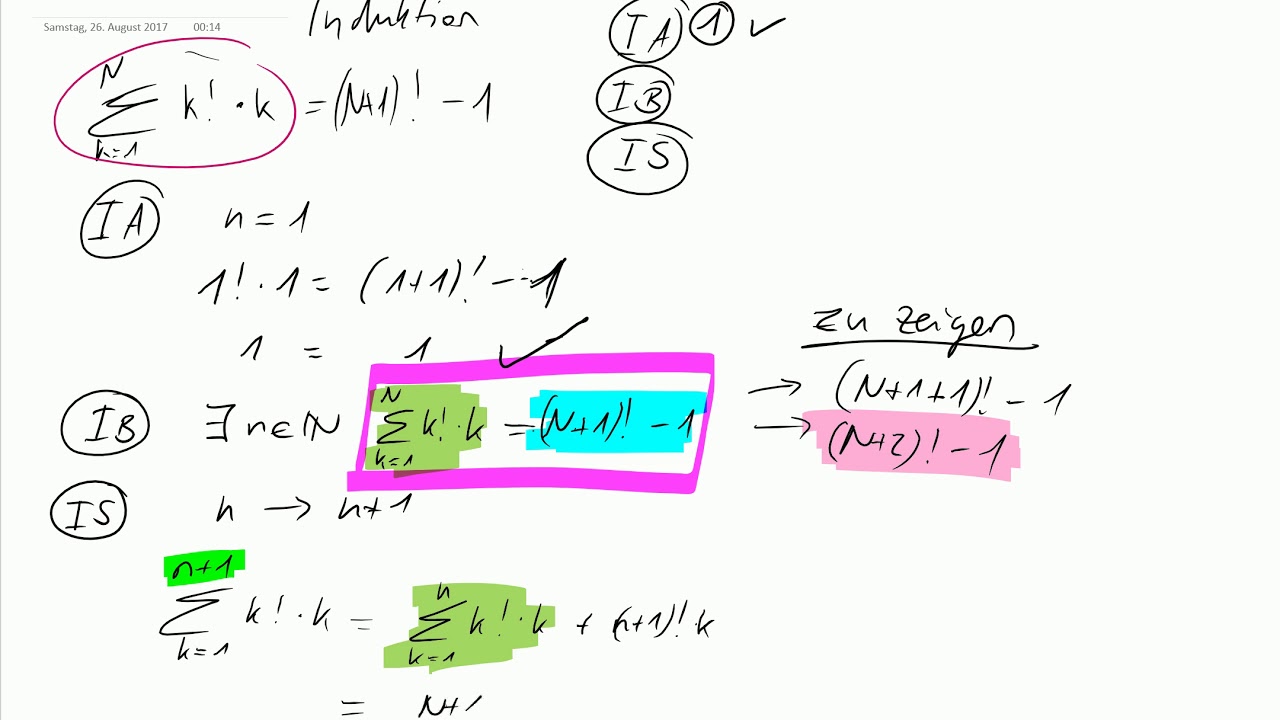
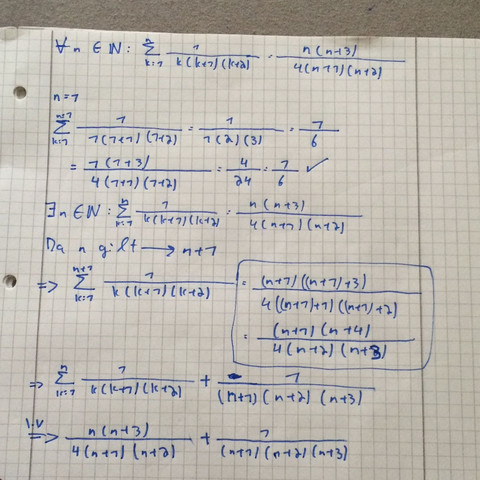
Induktion mathe beispiel. Vollständige induktion die vollständige induktion ist eine beweismethode um eine für alle natürliche zahlen formulierte aussage zu beweisen. K 1 2 n 1 1 k n 2. 1 n2 n ist gerade d h.
Im induktionsschritt is versuchen wir nun die aussage basierend auf der induktions voraussetzung auch für n 1 n 1 zu zeigen. Sum i 1 2 1 2 3. Ein beispiel ein schönes beispiel bei dem man vollständige induktion verwenden kann ist die gaußsche summenformel.
A 1 a 0. Aussage stimmt dies lässt sich bis unendlich theoretisch fortführen. Hier findet man erklärungen und aufgaben mit lösungen zum thema vollständige induktion.
Wir zeigen dass die formel für n 1 richtig ist. Beispiel für die vollständige induktion. 1 3 5 2n 1 n2 für alle n 2n.
K 1 2 n 1 1 1 k n 1 2. K 2 n 1 2 k k 1 1 3 1 2 n displaystyle prod k 2 n left 1 frac 2 k cdot k 1 right frac 1 3 cdot left 1 frac 2 n right. Sum i 1 3 1 2 3 frac 3 3 1 2 6.
A n 1 p a n 6 n 2n a 0 1. Displaystyle sum k 1 2 n 1 1 frac 1 k geq frac n 1 2. Frac 2 2 1 2 3.
Die vollständige induktion wird gerne genutzt um aussagen über reihen und folgen zu beweisen. Ist die zu beweisende aussage zum beispiel eine gleichung oder ungleichung so formen wir den linken teil der gleichung für n 1 n 1 so um dass ein teil genau den linken teil der gleichung für. A n 1 a n aus der.
Um den beweis zu erbringen geht man folgendermaÿen vor. N 1 a 1 p a 0 6 1 6 p 7 1 d h. Aussage stimmt n 3.
Begin align sum k 1 1 k 1 frac 2 2 frac 1 1 1 2 end align. P n i 1 2i 1 n2 d h. 2 n3 2n ist durch 3 teilbar.
Wir nehmen an dass a n a n 1 f ur irgend ein n 2n induktionsschluss. Aufgaben zur vollst andigen induktion wenn nichts anderes angegeben ist dann gelten die behauptungen f ur n 2 in f1 2 3 g. Für alle n 2n ist 32n 4 2n 1 durch 7 teibar.
Die summe aller ungeraden zahlen kleiner 2 n ist gleich n zum quadrat. 3 4n3 n ist durch 3 teilbar. 4 n3 n ist durch 6 teilbar.
Displaystyle sum k 1 2 n 1 frac 1 k geq frac n 2 ist dann ist. Für alle n geq 1 gilt sum k 1 n k frac n n 1 2. Als beispiel wollen wir folgende aussage beweisen.