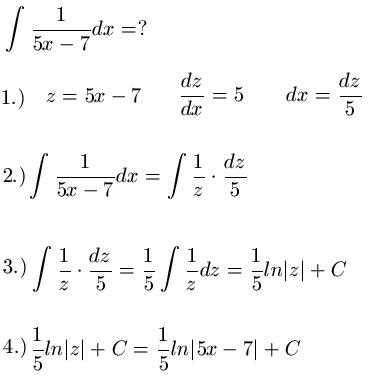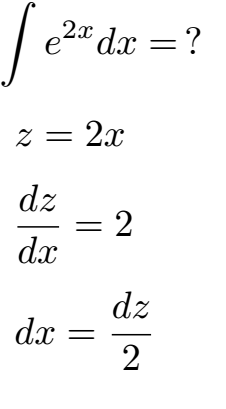Integration Substitution Beispiel

Arbeitsblatt Zur Stammfunktion Es Kann Als Faltblatt Und Ubungsblatt Kostenlos Auf Studimup De Gedownloadet Werden Nachhilfe Mathe Stammfunktion Mathe Formeln

Integration Durch Substitution

Pin By Heidi Jones On Breakout Edu Breakout Game Breakout Edu Games Breakouts

Was Sind Lineare Gleichungssysteme Was Ist Ein Lgs Lineare Gleichungssysteme Mit 2 Unbekannten Gleichungssysteme Gleichung Und Mathe

Im ersten beispiel soll ein bruch integriert werden.

Integration substitution beispiel. Allow for removal by moderators and thoughts about future. Es müsste also gelten. Beispiele zur substitution bei der integration anhand dieser vier punkte sollen nun einige beispiele zur integration durch substitution vorgerechnet werden.

Es gibt eine neue version dieses videos unter https youtu be t3wb432xon0 als 360 video aus dem hörsaal. Um f x per substitution zu integrieren müssen wir eine neue variable einführen u. Berechnen sie folgende integrale.

In diesem video rechne ich eine etwas schwerere aufgabe zur integration durch substitution bei der es vor allem nicht klar ist wie einem eine substitution. Browse other questions tagged calculus real analysis integration substitution or ask your own question. In unserem beispiel ersetzen wir 6x durch u sodass u 6x.

Integration durch substitution beispiel. Wir betrachten zum beispiel die funktion. Dann könnte man die funktion zu der funktion vereinfachen wollen.

Partialbruchzerlegung integration integration substitution integration substitution gegeben sei die funktion f x x5 1 x4. Das ist der fall wenn es sich um ineinander verschachtelte verkettete funktionen handelt. Z x5 1 x4 dx z t2 p t 1 t2 1 2 p t dt t x2 1 2 z 1 1 1 t2 dt t x2 1 2 t arctan t c t x2 1 2 x2 arctan x2 c.

Mit anschaulichen beispielen trainingsaufgaben integration durch substitution. Als faustregel kann man sich merken dass die integration durch substitution immer dann anzuwenden ist wenn man beim ableiten der funktion die kettenregel anwenden würde. Denn beispiele verdeutlichen die vorgehensweise in der regel am besten.

Diesen ausdruck kann man nun nach umstellen und nennt den erhaltenten term. Free math lessons and math homework help from basic math to algebra geometry and beyond. Featured on meta hot meta posts.

Berechnen sie das unbestimmte integral r f x dx mit der substitution x p t. Jetzt gilt nämlich was genau das ziel war. Students teachers parents and everyone can find solutions to their math problems instantly.

Bei φ φ handelt es sich um das kleine phi des griechischen alphabets.

Integration Durch Substitution An Diesem Beispiel Mathelounge

Integralrechnung Ubungen Und Aufgaben Mit Losungen Mathe Abitur Mathematik Tagliches Mathematik

Integration By Parts

Substitutionsregel Integration Durch Substitution