← Privater Geschaeftsbrief Beispiel Pruefmittelueberwachung Excel Vorlage R215 Richtig Ausfuellen Muster →
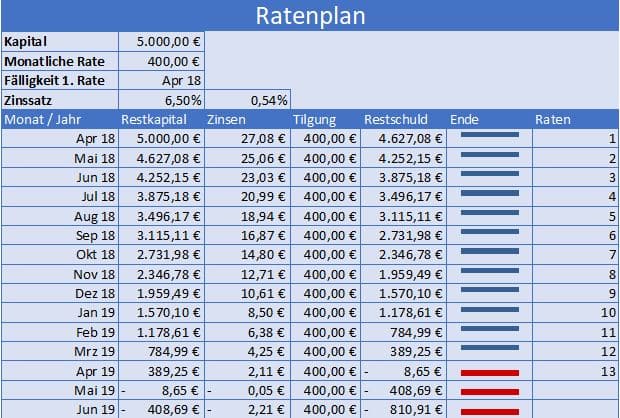
Ratenplan vorlage downloaden excel datei fazit zum ratenplan.
Ratenplan excel vorlage. Sparen dank kreditvergleich ob es tatsächlich erforderlich ist kredite explizit zu berechnen und deshalb den excel kreditrechner zu nutzen hängt ganz davon ab welche art von kredit benötigt wird und wie sich die einzelnen. Der innendienst kann den außendienst nbs. Laden sie eine excel tabelle mit einer tilgungsrechner für darlehen herunter um ihren eigenen amortisationsplan ihre eigene tabelle oder ihren eigenen taschenrechner zu erstellen.
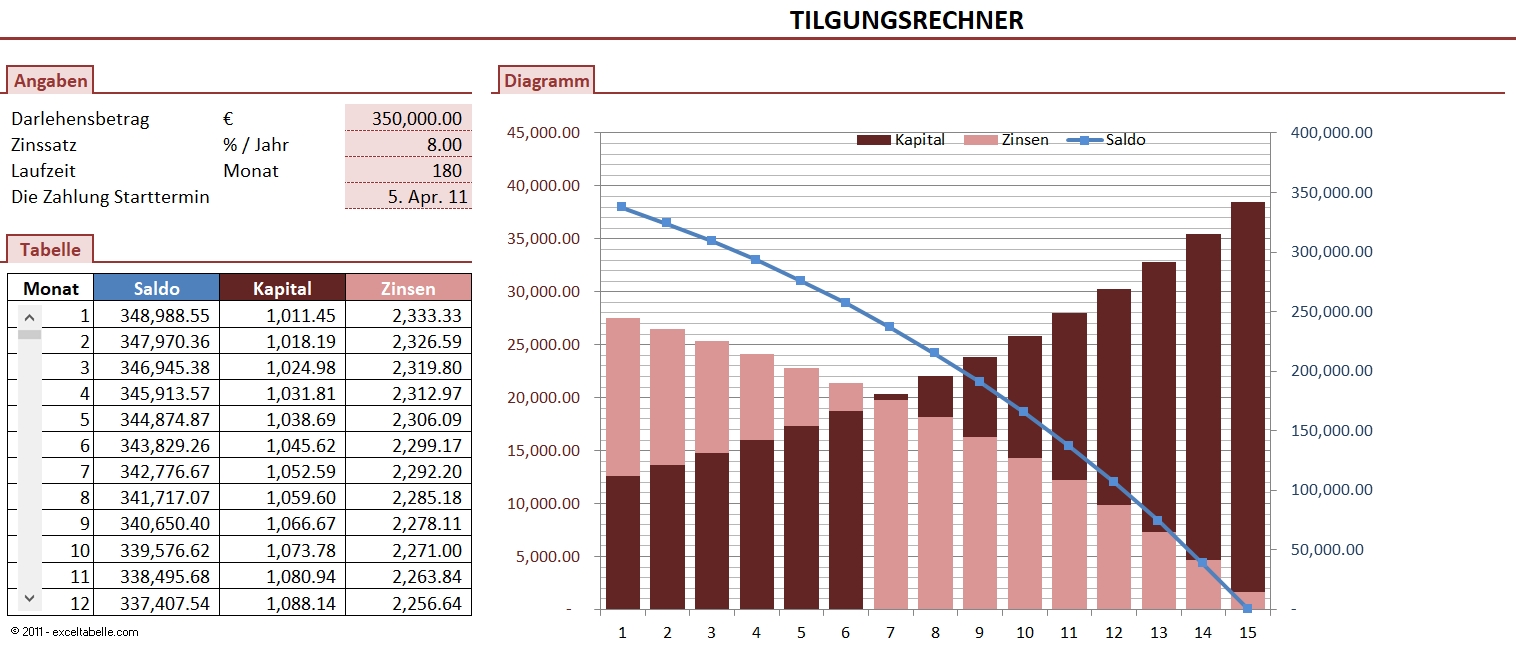
Durch den kredittilgungsplan wird dem nutzer die möglichkeit eingeräumt sich einen überblick über seine aufgenommenen kredite und deren tilgung zu verschaffen. Hier finden sie ein muster für eine ratenzahlungsvereinbarung die zwischen einem gläubiger und seinem schuldner zum vorläufigen verzicht auf vollstreckung geschlossen werden kann. Mit diesem darlehensrechner in excel wissen sie auf einen blick über die kreditsummen und zinszahlungen für jedes ihrer darlehen bescheid.
Dafür nutzen sie unsere vorlage prozesse zwischen innendienst und außendienst gestalten. Geben sie einfach die kreditsumme den zinssatz die kreditlaufzeit und das anfangsdatum in den excel darlehensrechner ein und alle monatlichen rückzahlungsraten und zinskosten bis zur endgültigen tilgung werden berechnet. Trotzdem mit ein wenig aufwand ist es auch mit excel möglich eine speisekarte zu erstellen.
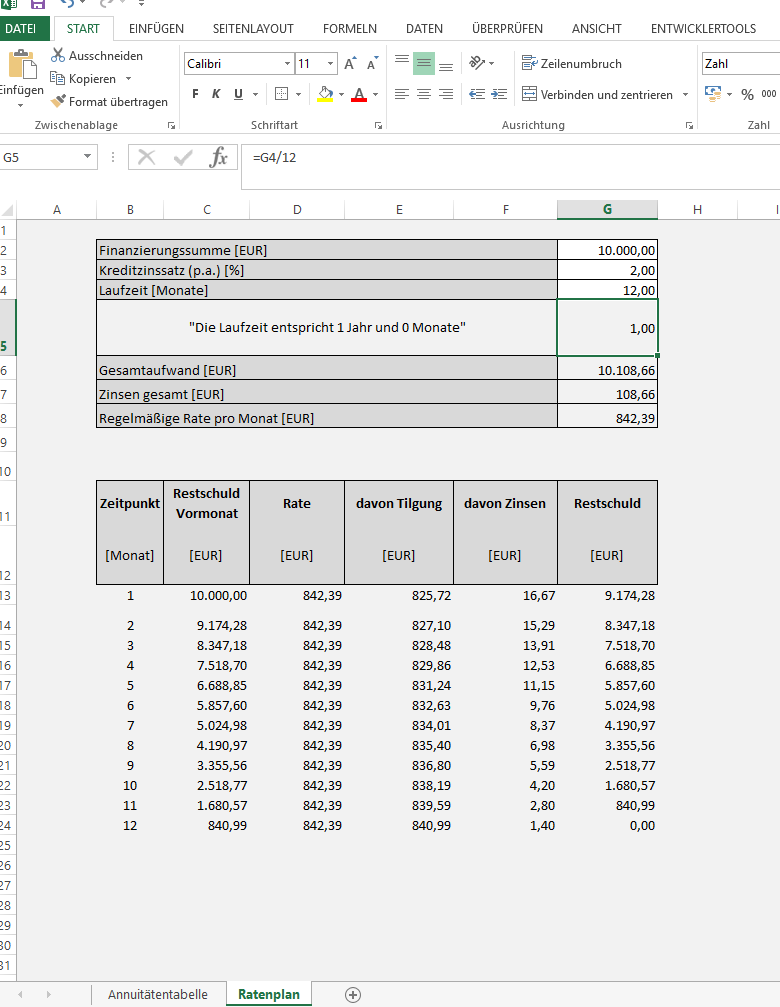
In excel zins und tilgungszahlungen berechnen. Kann der schuldner seinen zahlungsverpflichtungen nicht rechtzeitig oder in voller höhe nachkommen können ihm dadurch zusatzkosten in form von mahngebühren und ähnlichen kosten entstehen. Tatsächlich würde ich persönlich eher word oder gar indesign oder ein anderes layout programm dafür verwenden.
Behalten sie den überblick indem sie die richtigen finanzmathematischen funktionen von excel nutzen. Bemüht er sich jedoch darum. Vertriebsmanagement weil außendienst und innendienst eng zusammenarbeiten müssen die prozesse aufeinander abgestimmt sowie die aufgaben klar verteilt sein.
Sollten sie eine excel datei oder vorlage suchen mit der sich kredite berechnen lassen sind sie hier genau richtig.