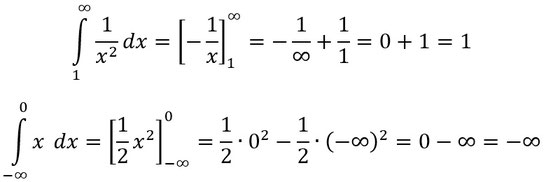← Urlaubsantrag Vorlage 2015 Uni Hamburg Powerpoint Vorlage Three Quarks For Muster Mark →
Satz sei f eine stetige funktion in a.
Mittelwertsatz der integralrechnung beispiel. Zwei mittelwertsätze der integralrechnung. Der zusatz für funktionen deren wertebereich ein intervall ist wie z. Mittelwertsatz der integralrechnung satz 15vj mittelwertsatz der integralrechnung sei f f f eine auf dem intervall.
Genauso wie es bei der differentialrechnung primär um die bestimmung der ableitung einer funktion geht beschäftigt sich die integralrechnung mit der bestimmung einer stammfunktion und den aussagen die man daraus schließen kann. Reelle analysis integration der mittelwertsatz der integralrechnung. Ein integral hat die folgende form die bezeichnungen.
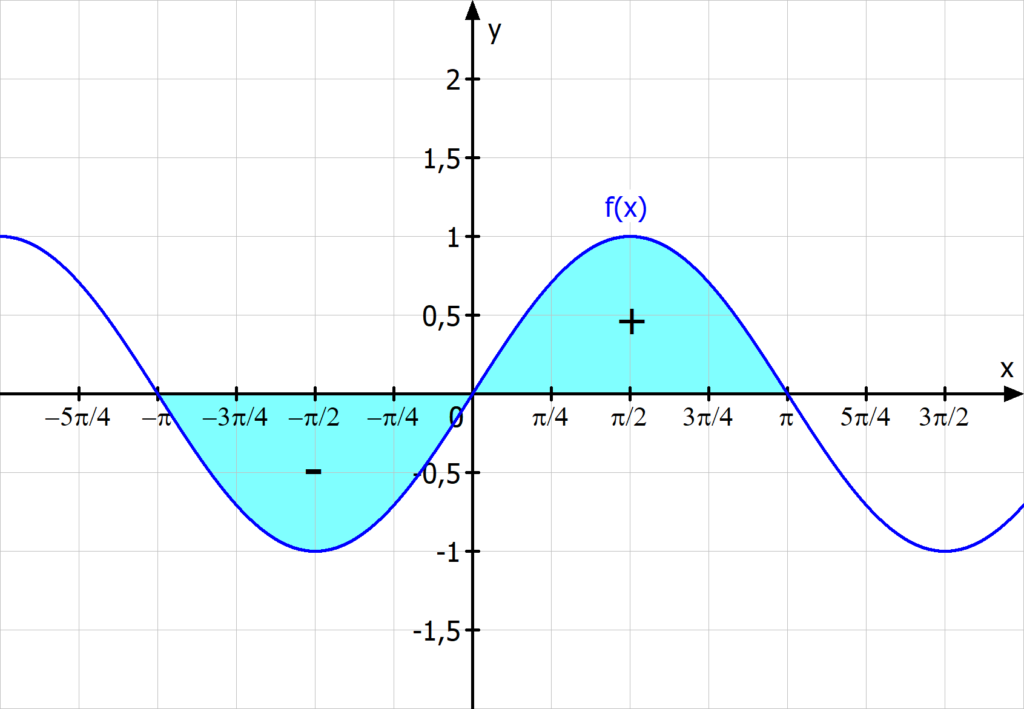
Min f a b zb a p. Visualisierung zum mittelwertsatz der integralrechnung. Aussagen über mittelwerteigenschaften des integrals.
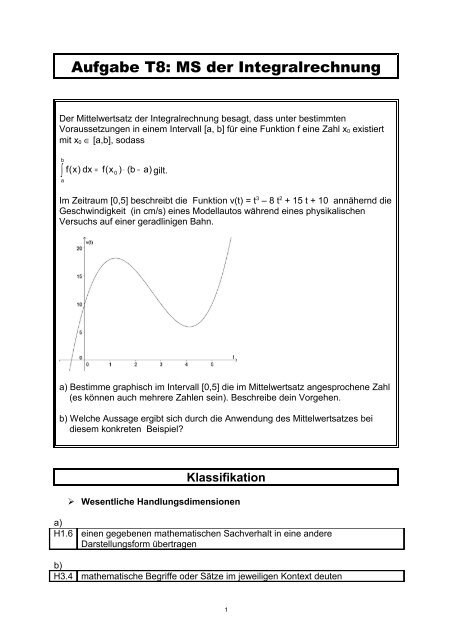
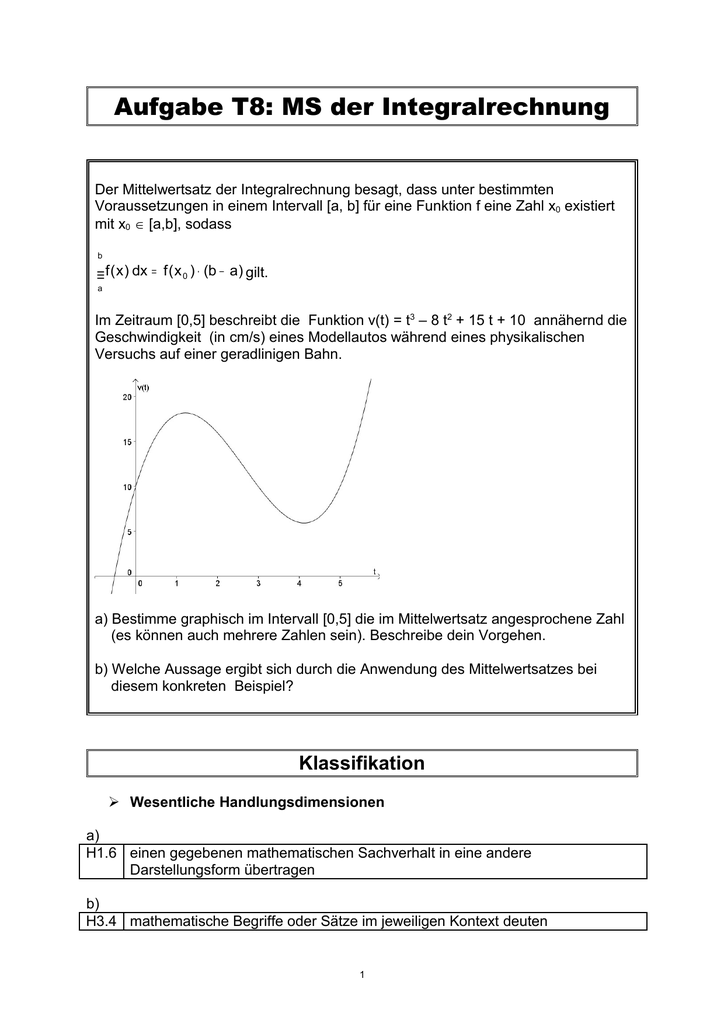
Sei f a b rstetig p a b rintegrierbar und p x 0 fu r a x b. Da f x stetig und p x 0 folgt. Dann existiert ein ξ a b mit zb a f x p x dx f ξ zb a p x dx.
Für stetige funktionen ergibt sich wenn wir s inf x a b f x und s sup x a b f x setzen die zweite version des mittelwertsatzes bringt eine nichtnegative sog. Wir können immer ein x 0 a b x 0 in a b x 0 a b finden so dass der flächeninhalt unter der kurve zwischen a a a und b b b dem eines rechtecks mit den seitenlängen b. B sodass der flächeninhalt des rechtecks gleich ist dem flächeninhalt unter der kurve von a bis b.
Die integralrechnung ist ein teilgebiet der analysis das eng mit der differentialrechnung verknüpft ist.