← Kuendigung Gitarrenunterricht Vorlage Kuendigung Pflegeheim Muster Kontaktliste Excel Vorlage →
Unter kurvendiskussion versteht man in der mathematik die untersuchung des graphen einer funktion auf dessen geometrische eigenschaften wie zum beispiel sch.
Natuerlicher kubischer spline beispiel. Dafür stellt man aus bedingungen ein lineares gleichungssystem bezüglich dieser unbekannten auf und löst es zum beispiel mit dem gauss verfahren. A die zugehörige lineare spline interpolationsfunktion s1 s1 b die zugehörige kubische spline interpolationsfunktion s3 s3. Aufgabe 6 spline bestimmung gegeben sei ein gitter x0 x1 x2 und die folgenden daten.
Bekannt ist aus ung03 4 dass die steigung des rechtssteitigen polynoms gleich dem linksseitigen polynom im. Glatte kurve bedeutet dabei im mathematischen sinne daß die kurve zweimal stetig differenzierbar sein soll. X i 0 1 2 f i 0 t 0 wobei t r.
Im cas erhalte ich darüberhinaus exakte ergebnisse. Die bekannte darstellung von kurven und flächen nach pierre bezier wird auf kubische und bikubische splines angewendet. Eine mit den spline bedingungen auf natürliche weise verbundene parameterdarstellung gestattet außerdem eine höchst einfache und übersichtliche korrektur der splines.
Jedes teilstück ist dabei durch eine kubische parabel a i x b i x c i x d i mit geeigneten koeffizienten a i b i c i und d i definiert. Zur weiteren beschreibung werden natürliche splines verwendet. In diesem beispiel geht es um die darstellung der grundsätzlichen überlegungen einen kubischen spline über abschnittsweise definierte kubische polynome zu beschreiben.
Hallo ich muss das interpolationspolynom ziwschen diesen 4 punkten bestimmen. Seien polynome 3 grades in wählt man den die enthalten die noch frei wählbaren koeffizienten für die bestimmung der zusammengesetzten kubischen spline funktion sind somit koeffizienten zu berechnen. Nun müssen die beiden unbekannten s i und s i 1 berechnet werden.
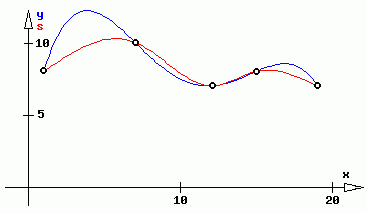
Ach ja fals sich manche fragen warum. Ein kubischer spline ist eine glatte kurve die durch gegebene punkte im koordinatensystem geht und eine minimale gesamtkrümmung aufweist. K ist der raum aller splines von grad k mit dim n k.
Bei der spline interpolation versucht man gegebene stützstellen auch knoten genannt mit hilfe stückweiser polynome niedrigen grades zu interpolieren während das ergebnis einer polynominterpolation durch unvorteilhaft festgelegte stützstellen oft bis zur unkenntlichkeit oszilliert liefert die splineinterpolation brauchbare kurvenverläufe und approximationseigenschaften rungephänomen. Das erste mal damit befasse vollkommen überfordert bin bräuchte mal die ganzen buchstaben in den formeln auf mein beispiel bezogen vllt kann ichs mir dann einprägen.
Source : pinterest.com
