← Lewis Saeure Beispiel Muster Arbeitsanweisung Zahnarzt Lerngeschichte Beispiel Malen →
Varianz oder auch kovarianz.
Regressionsgerade berechnen beispiel. Es gibt an wie viel prozent der varianz der abhängigen variable erklärt werden. Das r ist im intervall zwischen 0 und 1 definiert. Stell dir vor du möchtest einen freund zum geburtstag mit einem neuen paar schuhe überraschen.
Dies ist das modell einer so genannten einfachen linearen regression. Ziel bei den am häu figsten eingesetzten analyseverfahren ist es beziehungen zwischen einer abhängigen und einer oder. Regressionsanalyse die regressionsanalyse ist eine sammlung von statistischen analyseverfahren.
In dem beispiel ist das model signifikant mit einem p wert 0 001. Mit konstante wird der intercept a bezeichnet. Ein höherer wert ist hierbei besser.
Im falle der einfachen linearen regression stellt dies kein problem dar. Oben 4 0959 zu bestimmen oder man lässt dies mit der excel funktion mit f x wählen mit telwert bzw. Beispiele zur linearen regression 3 mit weniger komplizierten symbolen geschrieben sieht das so aus.
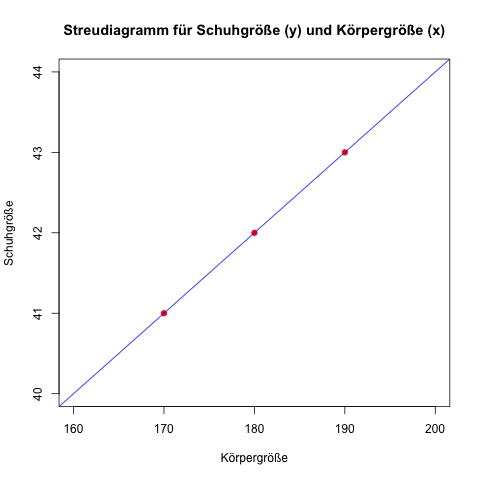
Lineare regression einfach erklärt viele beschreibende statistik themen üben für lineare regression mit videos interaktiven übungen lösungen. Dann berechnen wir mit der formel der regressionsgeraden die zugehörigen y werte. Im beispiel werden bei einem r von z b.
In unserem beispiel sind das deine aufzeichnungen vom letzten jahr also bei welcher temperatur wie viele gäste im schwimmbad waren. Die konstanten und nennen wir koe zienten oder parameter des modells. Leider kennst du jedoch seine schuhgröße nicht und bist deshalb unsicher welche schuhe du genau kaufen sollst.
0 5206 werden 52 06 der varianz der y variable erklärt. Somit ergibt sich im beispiel folgende regressionsgerade. Wir wollen sie aus den daten der studie bestimmen also sch atzen.
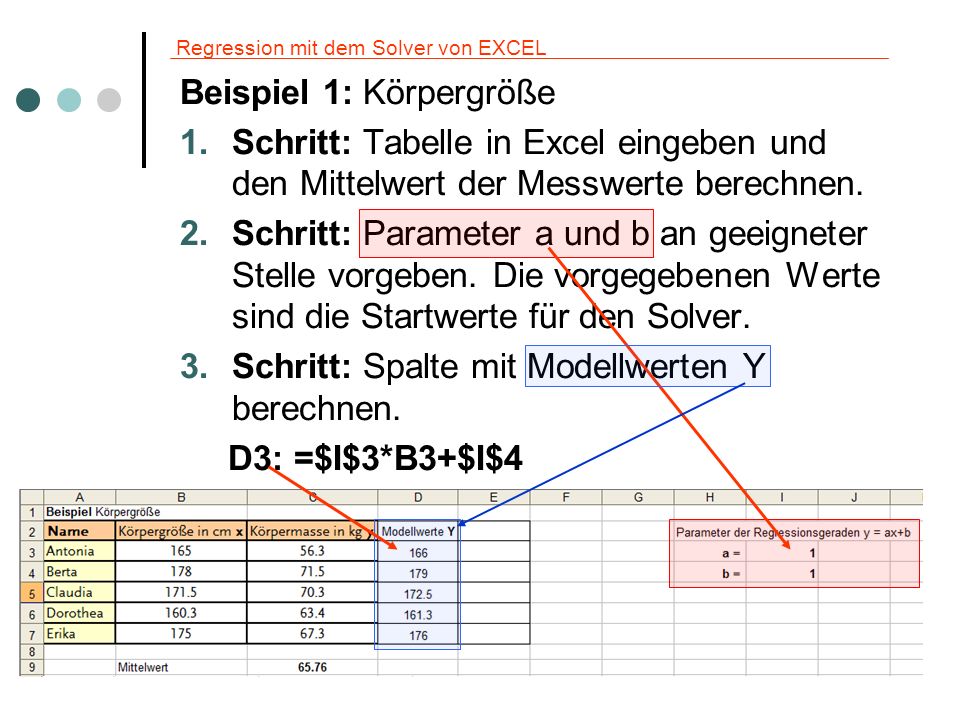
Prüfung der regressionskoeffizienten lässt sich die regressionsgerade in unserem beispiel berechnen. In diese punktwolke soll die regressionsgerade so hineingelegt werden dass sie möglichst nah an allen punkten liegt und so die daten möglichst gut abbildet. In dieser tabelle sind die schätzer für die regressionsgerade zu finden.
Mit hilfe der regressionskoeffizienten aus abbildung 7. Die konstante β0 ist in diesem modell nicht signifikant. Ihn direkt nach seiner schuhgröße fragen möchtest du nicht schließlich wäre dann die ganze überraschung kaputt.
2 8457 0 2836 cdot 160 48 22 2 8457 0 2836 cdot 170 51 06.
Source : pinterest.com
