← Ernährungsplan Schwangerschaft Beispiel Fadenbilder Vorlagen Kostenlos Einvernehmliche Auflösung Muster →
Dabei ist j a das trägheitsmoment des objekts in diesem fall einer kugel um den eigenen schwerpunkt m die masse des objekts und l der abstand des schwerpunkts von der drehachse.
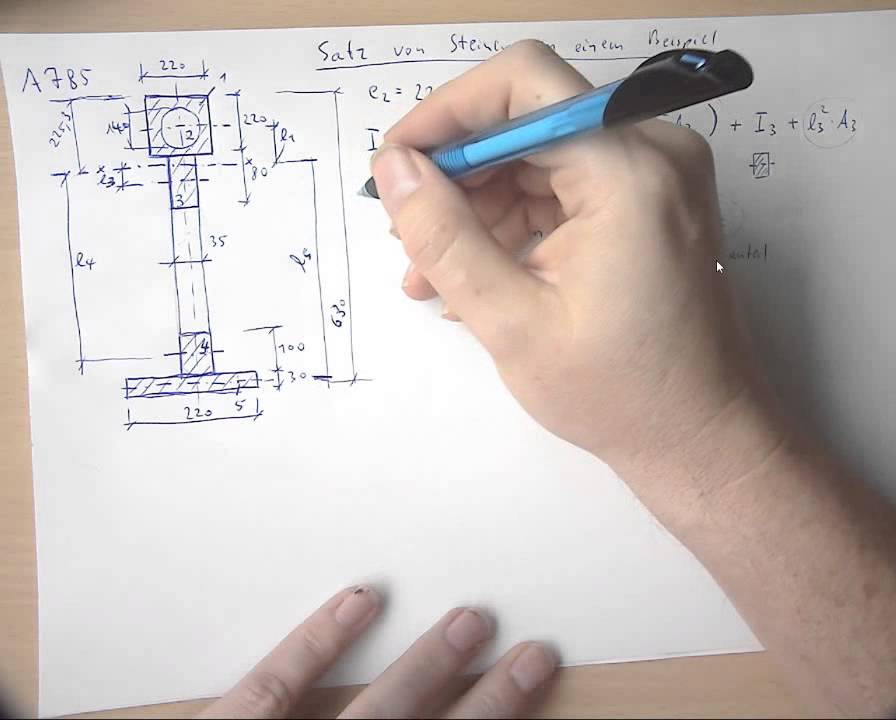
Satz von steiner beispiel. J j a m l 2. Immer auf eine bestimmte drehachse bezogen und hängt von der lage dieser achse im körperab. Berechnung des flächenschwerpunktes mit beispiel berechnung der standsicherheit sicherheit gegen kippen mit beispiel berechnung des flächenträgheitsmoments satz von steiner mit beispielen bzw.
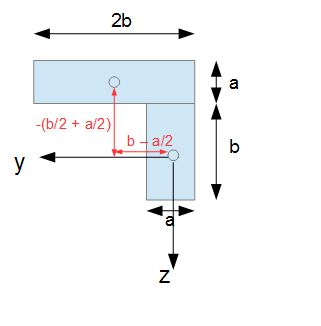
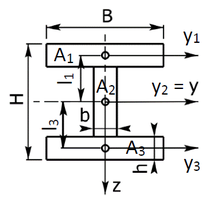
Die kreise in der skizze bezeichnen wieder die schwer punkte der teil flächen. Nach satz von steiner berechnet sich das trägheitsmoment j um eine rotationsachse wie folgt. A i i z sum i 1 n i z i sum i 1 n i z i y s i 2.
Die masse der kugeln ist gegeben. Flächen träg heits moment eines i profils mit satz von steiner es soll das flächen trägheits moment bezüglich der y achse wie in beispiel 2 berechnet werden diesmal jedoch mit dem satz von steiner. Für achsen parallel zur achse durch den schwerpunkt hat man einfach i a i s m r 2 wobei r der abstand sa ist.
Mit dem endergebnis um das massenträgheitsmoment des stabes um seine schwerpunktsachse zu bekommen kann man den satz von steiner anwenden. In diesem video erklärt dan was es mit dem satz von steiner auf sich hat den wir bei der berechnung von flächenträgheitsmomenten dann brauchen wenn wir da. Trägheitsmoment steiner scher satz torsionspendel zum nachweis des steiner schen satzes version vom 6.
Für j drei drei und j zwei drei versschwinden die steineranteile da der y abstand der einzelnen flächen zum schwerpunkt null ist. J z v r2 dm z v r2 ˆdv 1 formelzeichen einheit bezeichnung j kgm2 trägheitsmomentbzgl. Beispiele und berechnungen zum wirkungsgrad.
Der satz von steiner lautet wie folgt. Dieser besagt dass das massenträgheitsmoment jsum eine drehachse durch den schwerpunkt um m s vergrößert wird wenn sich die drehachse um den abstand s parallel verschiebt. J js ms 2.
Dafür addieren wir einfach die eigenmomente und die anteile nach dem satz von steiner der jeweiligen flächen zu einem gesamten flächenträgheitsmoment aufeinander auf. J 1 trägheitsmoment des körpers auf drehachse 1 schwerachse achse auf der sich der schwerpunkt des körpers befindet kg m 2 j 2 trägheitsmoment des körpers auf drehachse 2 kg m 2 md 2 steinersche anteil kg m 2. D h du kannst bei bekannter trägheit der kreisscheibe um s das trägheitsmoment um a schnell ausrechnen.
I y sum i 1 n i y i sum i 1 n i y i z s i 2.