← 5 Why Beispiel Antrag Auf Amtshilfe Muster Abmahnung Wegen Ruhestörung Muster →
36 moser reto f r f u tan 20 cos 20.
Torsion berechnen beispiel. Berechnung von achsen und wellen nach din 743. Mittelspannung zug druck σ zdm n mm 2 mittelspannung biegung σ bm n mm 2 mittelspannung torsion. Durchmesser wärmebehandlung d eff.
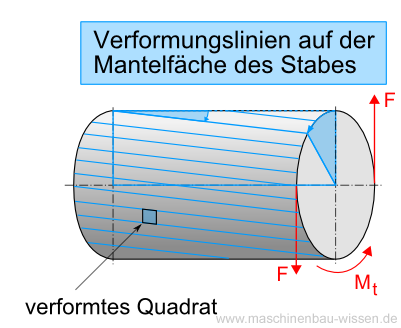
Bei einer torsion verdreht sich der körper. Neben diesen größen tritt bei torsion noch eine andere wichtige auf. Radius r mm.
Das torsionsmoment m x resultiert aus einer über den querschnitt verteilten schubspannung. Tau t max frac t w p le tau zul das widerstandsmoment. Rautiefe r z µm.
Die spannungen die bei diesem vorgang entstehen sind schubspannungen. Durchmesser d mm. Die torsion beschreibt die verdrehung eines körpers die durch die wirkung eines torsionsmoments entsteht.
Wie berechnet man nun die torsion. Es sind mehrere bereiche gegeben mit unterschiedlichen momentenwirkungen. 34 p t t w m τ polares widerstandsmoment für torsion formelbuch s.
W p frac j p r hier verwendet man zur berechnung der torsion den gleichungsaufbau wie bei kreisquerschnitten und bildet rechenwerte für. Torsion einer schraubenfeder für eine schraubenlinie mit der parameterdarstellung w t r cos t r sin t h t berechnen wir erst das kreuzprodukt p w x w wie in beispiel 1 p t h r sin t h r cos t r2. Torsion doc 08 10 20 seite 6 2 nachweise für torsion nach ec 2 2 1 nachweis für reine torsion der nachweis des grenzzustandes der tragfähigkeit erfolgt analog aller anderen nachweise.
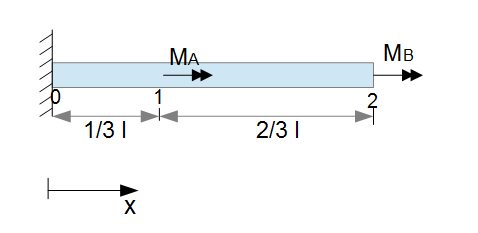
Aus dieser gleichung lässt sich wie im fall der biegung die gebrauchsformel ableiten. Im bereich overline 12 hingegen wirkt nur das torsionsmoment m b. Im bereich overline 01 wirken beide torsionsmomente m a und m b.
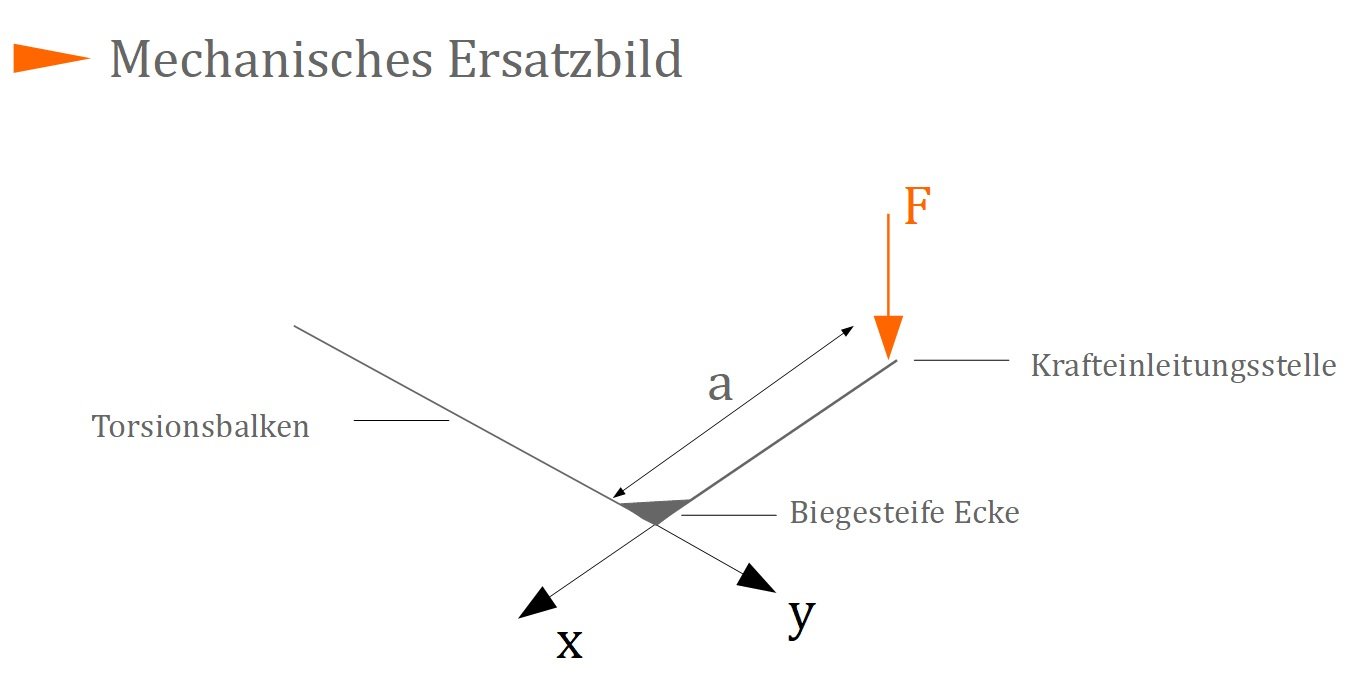
Durchmesser d mm. U b b b u b u b b u b r b f l cos f l m f tanl m f l f l 20 2 20 2 2 2 2 teilkreisd m t f u w m b σ b widerstandsmoment für biegung formelbuch s. Versucht man einen stab mit einem hebel senkrecht zur längsachse zu verdrehen so wirkt auf diesen ein torsionsmoment.
Für kreis und kreisringquerschnitte kann die verteilung der schubspannung einfach ermittelt werden. Dieses moment erzeugt in dem objekt spannungen welche als torsionsspannungen bezeichnet werden. Die kraft wirkt dabei über einen hebel und wird torsionsmoment genannt.
Torsion die belastung eines balkens durch ein moment um die x achse wird als torsion bezeichnet. Das infolge der belastungen einwirkende torsionsmoment muss kleiner oder gleich dem bauteilwiderstand bleiben der sich aus den zug und druckstreben ergibt. Tiefe t mm.
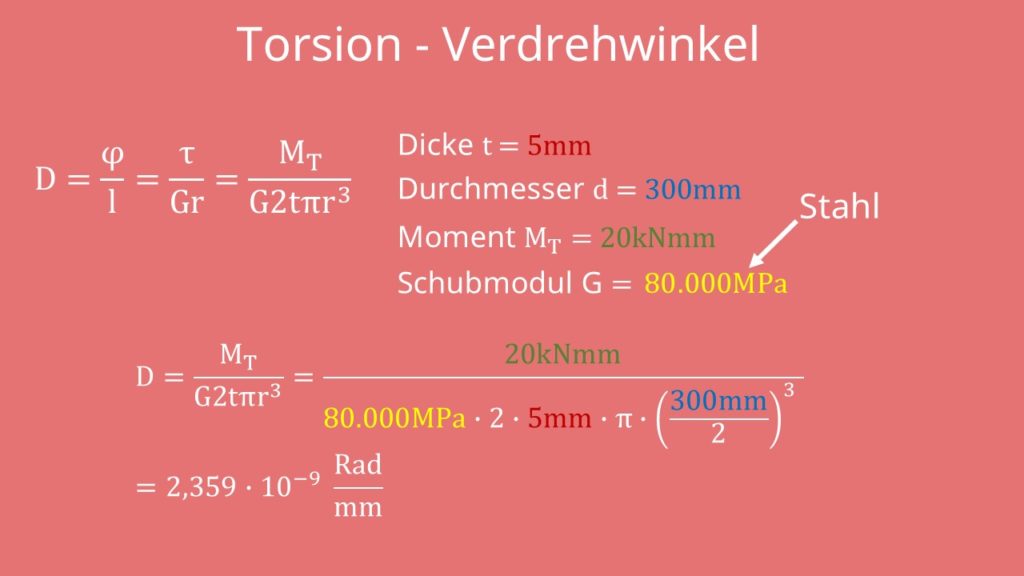
Dies wird mit der folgenden formel bei konstanter verdrillung vartheta beschrieben. Wir erhalten das torsionsmoment m t indem wir die kraft f mit länge r des eingesetzten hebels multiplizieren. Dies ist das drehmoment die berechnung der spannung und verformung erfolgt in den nächsten schritten.
Das torsionsmoment t displaystyle t ergibt sich aus der kraft f displaystyle f am hebel multipliziert mit der länge r displaystyle r des dazu verwendeten hebels. T f r displaystyle t f cdot r die entstehende verdrehung des stabs ergibt sich als.