← Barometrische Hoehenformel Beispiel Beschwerdebrief Pflegeheim Vorlage Aufsichtsübertragung Formular Vorlage →
Zudem kann man mit ihr die an einem bestimmten punkt im phasendiagramm maximal möglichen freiheitsgrade bestimmen.
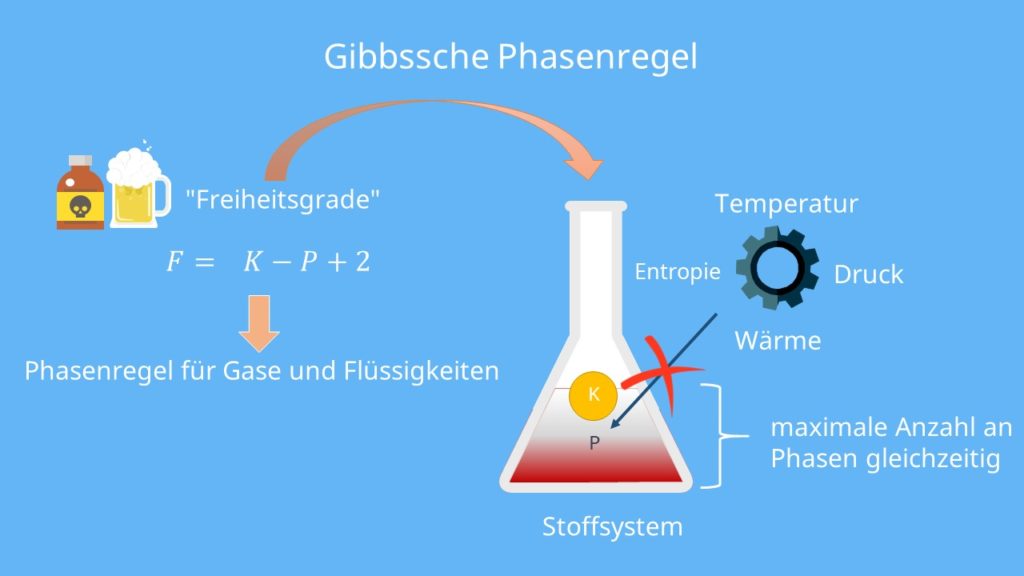
Gibbssche phasenregel beispiel. F k p 2 1 1 2 2. Somit ergibt sich die gibbssche phasenregel als. Die gibbssche phasenregel hält fest dass im thermodynamischen gleichgewicht nicht beliebig viele phasen gleichzeitig nebeneinander vorliegen können.
Die gibbssche phasenregel nach josiah willard gibbs 1876 auch einfach phasengesetz gibt an wie viele freiheitsgrade ein im thermodynamischen gleichgewicht befindliches system in abhängigkeit von der zahl der enthaltenen substanzen und der zahl der gleichzeitig existierenden phasen besitzt. Die gibbssche phasenregel nach josiah willard gibbs 1876 auch einfach phasengesetz hält fest dass im thermodynamischen gleichgewicht nicht beliebig viele phasen gleichzeitig nebeneinander vorliegen können. Beispielsweise liegt der tripelpunkt von kohlenstoffdioxid genau bei 216 55k was entspricht und 5180hpa.
Gibbssche phasenregel gibbssches phasengesetz thermodynamisch abzuleitender und durch die erfahrung bestätigter zusammenhang zwischen der anzahl p der phasen in einem sich im thermodynamischen gleichgewicht befindenden heterogenen system aus k komponenten und der anzahl f der thermodynamischen freiheitsgrade. Diamanten bestehen aus kohlenstoff k 1 in fester form p 1. Eingesetzt in die gibbs sche phasenregel ergibt sich die anzahl der zustandsgrößen die für die diamantenherstellung berücksichtigt werden müssen.
Für ein physikalisch homogenes thermodynamisches system reichen zwei. Die gibbssche phasenregel nach josiah willard gibbs 1876 beinhaltet die aussage dass im thermodynamischen gleichgewicht nicht beliebig viele phasen gleichzeitig nebeneinander vorliegen können. Anwendung der gibbs schen phasenregel.
Zudem kann man mit ihr die an einem bestimmten punkt im phasendiagramm maximal möglichen freiheitsgrade bestimmen. F 1 3 2 0 ein thermodynamischer freiheitsgrad von 0 bedeutet dass keine variation der größen druck oder temperatur möglich ist ohne die phasen mit zu verändern. Für ein physikalisch homogenes thermodynamisches system reichen zwei zustandsgrößen zur bestimmung des gleichgewichtszustands.
Source : pinterest.com